Properties of Continuous Function on Closed Interval

Abstract

Formal mathematics is getting increasing attention in mathematics and computer science. In particular, the formalization of calculus has important applications in engineering design and analysis. In this paper, we present a formal proof of some fundamental theorems of continuous functions on closed intervals based on the Coq proof assistant. In this formalization, we build a real number system referring to Landau's Foundations of Analysis. Then we complete the formalization of the basic definitions of interval, function, and limit and formally prove the theorems including completeness theorem, intermediate value theorem, uniform continuity theorem and others in Coq. The proof process is normalized, rigorous and reliable.

Keywords

• Coq
• Formalization
• Limits
• Continuous functions
• Closed intervals

This research is supported by National Natural Science Foundation (NNSF) of China under Grant 61936008, 61571064.

1 Introduction

Analysis is one of the greatest achievements in the history of mathematics. The achievement opens a new era of mathematical progress and plays an important role in development of physics, astronomy, signal processing and other disciplines. Analysis which evolved from calculus is a branch of mathematics that studies limits and related theories [12].

At the end of the 19th century, mathematicians deduced many properties of continuous functions on closed intervals, which undoubtedly promoted the development of analytical theory. There are some important properties of continuous functions on closed intervals including Weierstrass second theorem: Boundedness theorem, Weierstrass first theorem: Extreme value theorem, Bolzano-Cauchy second theorem: Intermediate value theorem, Cantor theorem: Uniform continuity theorem.

Bolzano's Function Theory gives the earliest proofs of the Boundedness theorem and the Extreme value theorem (but published some 100 years later) [15], and Weierstrass proved the Extreme value theorem in Berlin lecture. The Intermediate value theorem was first proved in 1817 by Bolzano, and then Cauchy [7] gave a proof in 1821. The definition of uniform continuity is proposed by Heine, and he published a proof of the Uniform continuity theorem.

With the further research of limits by mathematicians, the establishment of a rigorous and complete system of real numbers theory has become a key issue. In 1872, three major real numbers theories appeared in Germany: Dedekind cut theory, Cantor-Henie-Meray "basic sequence" theory, and Weierstrass "bounded monotone sequence" theory. Among them, the Dedekind cut is particularly recognized, and it is called the creation of human intelligence that does not rely on the intuitiveness of space and time. Then Peano established a natural number theory through a set of axioms, thereby solving the core problems of rational number theory and also the basic problems of real number theory.

In recent years, with the rapid development of computer science, especially the emergence of proof assistant Coq, Isabelle and HOL Light and so on [2, 4, 8, 10, 14, 17], formal proof of mathematical theorems has made great progress. In 2005, the international computer experts Gonthier and Werner provided the formal proof in Coq of the famous "four-color theorem" successfully [5]. After years of hard work, Gonthier again achieved the machine proof in Coq of the "odd order theorem" in 2012 [6]. Those progress make Coq more and more popular in academia. Wiedijk pointed out that relevant research teams around the world have completed or plan to formalize the proof of theorems such as Gödel's first incompleteness theorem, Jordan curve theorem, Prime theorem and Fermat last theorem of a hundred well-known mathematical theorems [17].

Based on "Real number theory" formal system, we formalize the properties of continuous functions on closed intervals. Moreover, we give formal proofs of these theorems, which include the Boundedness theorem, the Extreme value theorem, the Intermediate value theorem, the Uniform continuity theorem. It should be noted that the properties of continuous functions on closed intervals is an important theorem in analysis.

The structure of this article is as follows: In Sect. 2, we introduce the "real number theory" machine proof system. In Sect. 3, we present the formal definition of the function limit and related properties. In Sect. 4, we discuss the machine proof of the properties of continuous functions on closed intervals in detail, which are derived by supremum theorem. In Sect. 5, we draw conclusions and discuss some potential further work.

2 Real Number Theory System

Before formally proving the properties of continuous functions on closed intervals, we first need to build a formal system of real number theory. van Benthem Jutting [1] completed the formalization in Automath of Landau's "Foundations of Analysis", which was a significant early progress in formal mathematics. Harrison [9] presents formalized real numbers and differential calculus on his HOL Light system. The definition of real numbers in Coq standard library uses the axiomatic way, and based on this, excellent real analysis library Coquelicot [3] has been established. This library accomplishes many achievements, but its definition of real number is non-constructive. Hornung [11] completed the first four chapters of the "Foundations of Analysis" in Coq, which is closed related to our work, however our system is closer to the expression of Landau and more readable. We also completed the complex number part and proved equivalence between eight completeness theorems of real number.

There are several ways to define natural numbers in Coq. Based on Morse-Kelley axiomatic set theory, it is designed to give quickly and naturally a foundation for mathematics, and meanwhile deduce the Peano axioms as theorems [16, 18]. If we start from the more higher type rather than set theory, we can formalize straight Peano axioms as follows:

Based on this, we can use "Parameter" and "Axiom" to define natural number related functions such as addition and multiplication. This way is intuitive but not elegant. The natural numbers defined by "Inductive" can recursively define natural number related functions.

Landau's "Foundations of Analysis" [13] is based on naive set theory and some basic logic. Starting from the Peano axioms, natural numbers (positive integers), fractions (positive), rational numbers/integer (positive) are defined in order. The real number, defined by Dedekind cut, defines complex numbers through real numbers for constructing systematically the whole number system theory. We have completed the Coq formalization of the system, and the complete source is available online:

In this system, we can prove Dedekind fundamental theorem, and derive Supremum theorem. The proof details are not described, and the formalization is as follows.

2.1 Dedekind Fundamental Theorem

Divide all real numbers into two classes, so that the first class and second class are not empty, and each number in the first class is less than each number in the second class. Then there is a unique real number E, so that any number less than E belongs to the first class, and any number greater than E belongs to the second class.

2.2 Supremum Theorem

If a non-empty real number set has a upper bound, then there must be a least bound (the Supremum as an example).

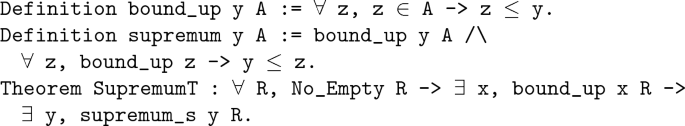
3 Basic Definitions and Properties

The formal definition of functions in this system is as follows:

Related definitions of function continuity:

The function f(x) is continuous at one point implying that

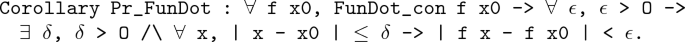
The function f(x) is continuous (left, right) at a point, then the function f(x) is locally bounded at this point (take right continuous for example):

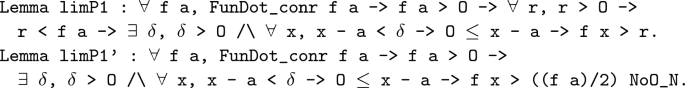
In this real number system, division function requires three parameters, and the third of which is the proof that the second is not 0. Therefore, the "NoO_N" above means "\(2 \ne 0\)".

The function f(x) is continuous on [a,b], then \(-f (x)\) is continuous on [a,b]. The function f(x) is continuous on [a,b] and is not everywhere 0, then \(\frac{1}{f(x)}\) is continuous on (take \(f(x)> 0\) as an example).

4 Properties of Continuous Functions on Closed Intervals

Continuous functions have four fundamental properties on closed intervals: Boundedness theorem (Weierstrass second theorem), Extreme value theorem (Weierstrass first theorem), Intermediate value theorem (Bolzano-Cauchy second theorem), Uniform continuity theorem (Cantor theorem). These theorems are the basis of mathematical analysis and the direct expression of real number theory in functions. Our formalizations rely on a logical axiom law of excluded middle.

Theorem 1

Boundedness theorem: A continuous function on a closed interval must be bounded on that interval.

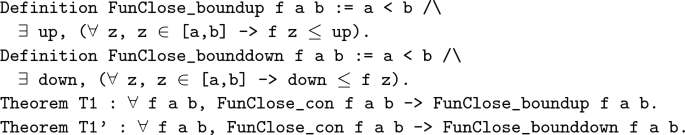
First, we prove a lemma L1: if f(x) is continuous on [a,b], then some neighborhood of z is bounded for any \(z \in (a,b)\). The notation "\([x0|-\delta ]\)" below represents \(U_{x_0}(\delta )\) in mathematics.

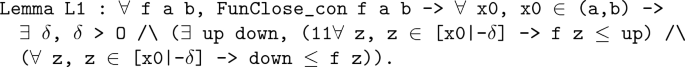
Upper bound: Construct a real number set \(\{t: f(x)\) has an upper bound on \([a, t] \}\). The formal definition is as follows:

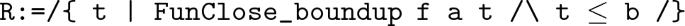
As f(x) is right continuous at the point a, there exists \(\delta > 0\), and f(x) has an upper bound on \((a, a + \delta )\), when \(b \le a + \delta \) proves the proposition. When \(a + \delta < b\), R is not empty. On the other hand, b is an upper bound of R obviously, so R has supremum \(\xi \), and \(\xi \le b\).

Case 1(\(\xi <b\)): According to Lemma L1, there exists \(\delta _1> 0\), and f(x) has an upper bound on \((a, \xi + \delta _1)\). The proposition is proved when \(b <\xi + \delta _1\). When \(\xi + \delta _1 \le b\), there is \(\xi + \delta _1 \in R\), which contradicts \(\xi \) is the supremum of R.

Case 2(\(\xi = b\)): The proposition is proved because of \(b <\xi + \delta _1\).

Lower bound: According to the lemma Pr_fun1, it can be deduced that \(-f(x)\) is continuous on [a,b]. From Theorem T1, we know that \(-f(x)\) has the upper bound "up", then "-up" is the lower bound of f(x) on [a,b].

Theorem 2

Extreme value theorem: The continuous function on the closed interval must achieve the maximum and minimum values in this interval.

Maximum value: Construct a real number set \(\{f(x): x \in [a, b] \}\). The formal definition is as follows:

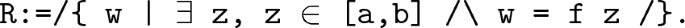
Obviously, R is not empty and we can deduce R has an upper bound by T1, hence R has a supremum M. If there exists \(x \in (a, b)\) and \(f(x) = M\), the proposition is proved. Otherwise, \(f(x) < M\) for any \(x \in [a, b]\). Construct a new function \(g(x) = \frac{1}{M-f (x)}\). Since \(g(x) > 0\) for any \(x \in \) [a, b], so g(x) is continuous on [a,b] by Pr_fun2. From T1, g(x) has an supremum K on [a,b], and \(K > 0\). After derivation, \(M- \frac{1}{K}\) is the upper bound of f(x) on [a,b], which contradicts M is the supremum of R.

Minimum value: According to the lemma Pr_fun1, it can be deduced that \(-f(x)\) is continuous on [a,b]. From Theorem T2, we know that \(-f(x)\) has a maximum value "max", then "-max" is the minimum value of f(x) on [a,b].

Theorem 3

Intermediate value theorem: If \(f(a) \ne f(b)\), then for any real number C between f(a), f(b), at least one point c on (a,b) satisfies f (c) = C.

First, we prove a lemma L3: if f(x) is left continuous at point b, \(a <b\) and \(f(b)> C\), then there is z between a,b, satisfies \(f(z) > C\).

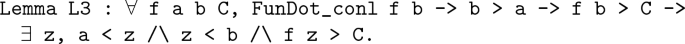
\(f(a)< f(b)\): Construct a real number set \(\{t: f(x) < C\) for any x in \([a, t] \}\). The formal definition is as follows:

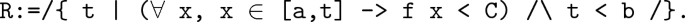
\(f(a)> f(b)\): f(x) is right continuous at point a, then there exists \(\delta _1> 0\), and \(|f(x) - f(a)|< C - f(a)\) in \((a, a + \delta _1)\), which can be deduced \(f(x) < C\). \((a+\frac{\delta _1}{2}) \in R\) when \(\delta _1 <(b - a)\) and \(\frac{a + b}{2} \in R\) when \((b - a) \le \delta _1\). In summary, R is not empty and b is an upper bound of R, so R has a supremum \(\xi \), and \(\xi \le b\). When \(\xi = b\), it can deduce contradiction according to Pr_supremum and L3. Therefore \(\xi \in (a, b)\).

Case 1(\(f(\xi ) <C\)): Because f(x) is continuous at point \(\xi \), by Pr_FunDot there is \(\delta > 0\), and \(| f(x)-f(\xi ) | <\frac{C-f(\xi )}{2}\) for any \(x \in [\xi - \delta , \xi + \delta ]\), which can be deduced \(f(x) <C\). Further, we can conclude that \((\xi + \delta ) \in R\) which contradicts \(\xi \) is the supremum of R.

Case 2(\(f(\xi )> C\)): f(x) is continuous at point \(\xi \), hence f(x) is left continuous at point \(\xi \). By L3 there must exist \(z \in (a, \xi )\) and \(f (z)> C\), so z is the upper bound of R, which contradicts \(\xi \) is the supremum of R.

\(f(a)> f(b)\): Refer to T1', T2' proof.

Theorem 4

Uniform continuity theorem: A function is continuous on a closed interval then the function is uniformly continuous on that interval.

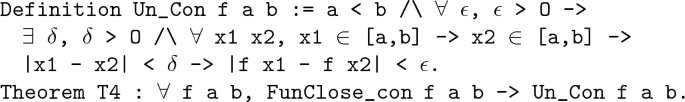
Let f(x) be continuous on [a,b], fix any \(\epsilon> 0\). we construct a real number set \(\{t: \exists \delta > 0\) and \(| f(x_1)-f(x_2) | <\epsilon \) when \(x_1, x_2 \in [a, t]\) and \(| x_1-x_2 | \le \delta \}\). The formal definition is as follows:

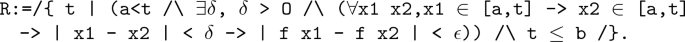
Because f(x) is right continuous at point a, there must exists \(\delta _1> 0\), and \(| f(x)-f(a) | <\frac{\epsilon }{2}\) for any \(x \in [a, a + \delta _1)\). Let \(\delta _2 = min (a + \frac{\delta _1}{2}) (b-a)\), we prove that \(a + \delta _2 \in R\). Obviously, b is an upper bound of R, So R has a supremum \(\xi \) and \(\xi \le b\). As f(x) is continuous at point \(\xi \), there exists \(\delta > 0\), and \(| f(x) -f (\xi ) | <\frac{\epsilon }{2}\) for any \(x \in [\xi - \delta , \xi + \delta ]\). Further, we can deduce \(| f (x_1)-f (x_2) | <\epsilon \) for any \(x_1, x_2 \in [\xi - \delta , \xi + \delta ]\). Therefore, \(| f(x_1)-f(x_2) | <\epsilon \) for any \(x_1, x_2 \in [a, \xi + \delta ]\) and \(| x_1-x_2 | \le \delta \).

Case 1(\(\xi <b\)): When \(b <\xi + \delta \), the proposition is proved due to the arbitrariness of \(\epsilon \). When \(\xi + \delta \le b\), we further prove \(\xi + \delta \in R\), which contradicts \(\xi \) is the supremum of R.

Case 2(\(\xi = b\)): \(b <\xi + \delta \), the proposition is proved by the arbitrariness of \(\epsilon \).

5 Conclusion

This paper formalizes limits, continuous functions and related theorems. These theorems include Boundedness theorem, Extreme value theorem, Intermediate value theorem, and Uniform continuity theorem. We have completed their formal proofs based on the real number theory system developed by ourselves. In the future, we will formalize more theorems of continuous functions and make meaningful attempts for formal work in the fields of real analysis and complex analysis. We are grateful to the anonymous reviewers, whose comments much helped to improve the presentation of the research in this article.

References

1. van Benthem Jutting, L.S.: Checking Landau's "Grundlagen" in the AUTOMATH System. North-Holland, Amsterdam (1994)

   MATH  Google Scholar

2. Bertot, Y., Castéran, P.: Interactive Theorem Proving and Program Development: Coq'Art: The Calculus of Inductive Constructions. Texts in Theoretical Computer Science An EATCS Series. Spring-Verlag, Heidelberg (2004). https://doi.org/10.1007/978-3-662-07964-5

   CrossRef  MATH  Google Scholar

3. Boldo, S., Lelay, C., Melquiond, G.: Coquelicot: a user-friendly library of real analysis for Coq. Math. Comput. Sci. 9(1), 41–62 (2015). https://doi.org/10.1007/s11786-014-0181-1

   MathSciNet  CrossRef  MATH  Google Scholar

4. Chlipala, A.: Certified Programming with Dependent Types: A Pragmatic Introduction to the Coq Proof Assistant. MIT Press, Cambridge (2013)

   CrossRef  Google Scholar

5. Gonthier, G.: Formal proof-the four-color theorem. Notices AMS 55(11), 1382–1393 (2008)

   MathSciNet  MATH  Google Scholar

6. Gonthier, G., et al.: A machine-checked proof of the odd order theorem. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 163–179. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39634-2_14

   CrossRef  Google Scholar

7. Grabiner, J.V.: Who gave you the epsilon? Cauchy and the origins of rigorous calculus. Am. Math. Mon. 90(3), 185–194 (1983)

   MathSciNet  CrossRef  Google Scholar

8. Hales, T.C.: Formal proof. Notices AMS 55(11), 1370–1380 (2008)

   MathSciNet  MATH  Google Scholar

9. Harrison, J.: Theorem Proving with the Real Numbers. Springer, Heidelberg (1994)

   MATH  Google Scholar

10. Harrison, J.: Formal proof—theory and practice. Notices AMS 55(11), 1395–1406 (2008)

    MathSciNet  MATH  Google Scholar

11. Hornung, C.: Constructing Number Systems in Coq. Saarland University, Saarbrücken (2011)

    Google Scholar

12. Katz, V.J.: A History of Mathematics. Pearson/Addison-Wesley, Boston (2004)

    MATH  Google Scholar

13. Landau, E.: Foundations of Analysis: The Arithmetic of Whole, Rational, Irrational, and Complex Numbers. Chelsea Publishing Company, New York (1966)

    Google Scholar

14. Nipkow, T., Wenzel, M., Paulson, L.C. (eds.): Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9

    CrossRef  MATH  Google Scholar

15. Rusnock, P., Kerr-Lawson, A.: Bolzano and uniform continuity. Historia Mathematica 32(3), 303–311 (2005)

    MathSciNet  CrossRef  Google Scholar

16. Sun, T., Yu, W.: A formal system of axiomatic set theory in Coq. IEEE Access 8, 21510–21523 (2020)

    CrossRef  Google Scholar

17. Wiedijk, F.: Formal proof-getting started. Notices AMS 55(11), 1408–1414 (2008)

    MathSciNet  MATH  Google Scholar

18. Yu, W., Sun, T., Fu, Y.: Machine Proof System of Axiomatic Set Theory. Science Press, Beijing (2020)

    Google Scholar

Download references

Author information

Authors and Affiliations

1. Beijing Key Laboratory of Space-Ground Interconnection and Convergence School of Electronic Engineering, Beijing University of Posts and Telecommunications, Beijing, 100876, China

   Yaoshun Fu & Wensheng Yu

Corresponding authors

Correspondence to Yaoshun Fu or Wensheng Yu .

Editor information

Editors and Affiliations

1. Dipartimento di Matematica, Università degli Studi di Genova, Genova, Genova, Italy

   Anna Maria Bigatti

2. Computing and Software, McMaster University, Hamilton, ON, Canada

   Jacques Carette

3. Department of Computer Science, University of Bath, Bath, UK

   James H. Davenport

4. Institut für Mathematik, MA 6-2, TU Berlin, Berlin, Germany

   Prof. Michael Joswig

5. Technische Universität Braunschweig, Braunschweig, Germany

   Timo de Wolff

Rights and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this paper

Cite this paper

Fu, Y., Yu, W. (2020). A Formalization of Properties of Continuous Functions on Closed Intervals. In: Bigatti, A., Carette, J., Davenport, J., Joswig, M., de Wolff, T. (eds) Mathematical Software – ICMS 2020. ICMS 2020. Lecture Notes in Computer Science(), vol 12097. Springer, Cham. https://doi.org/10.1007/978-3-030-52200-1_27

Download citation

• .RIS
• .ENW
• .BIB

• DOI : https://doi.org/10.1007/978-3-030-52200-1_27

• Published: 08 July 2020

• Publisher Name: Springer, Cham

• Print ISBN: 978-3-030-52199-8

• Online ISBN: 978-3-030-52200-1

• eBook Packages: Computer Science Computer Science (R0)

garciathendous.blogspot.com

Source: https://link.springer.com/chapter/10.1007/978-3-030-52200-1_27